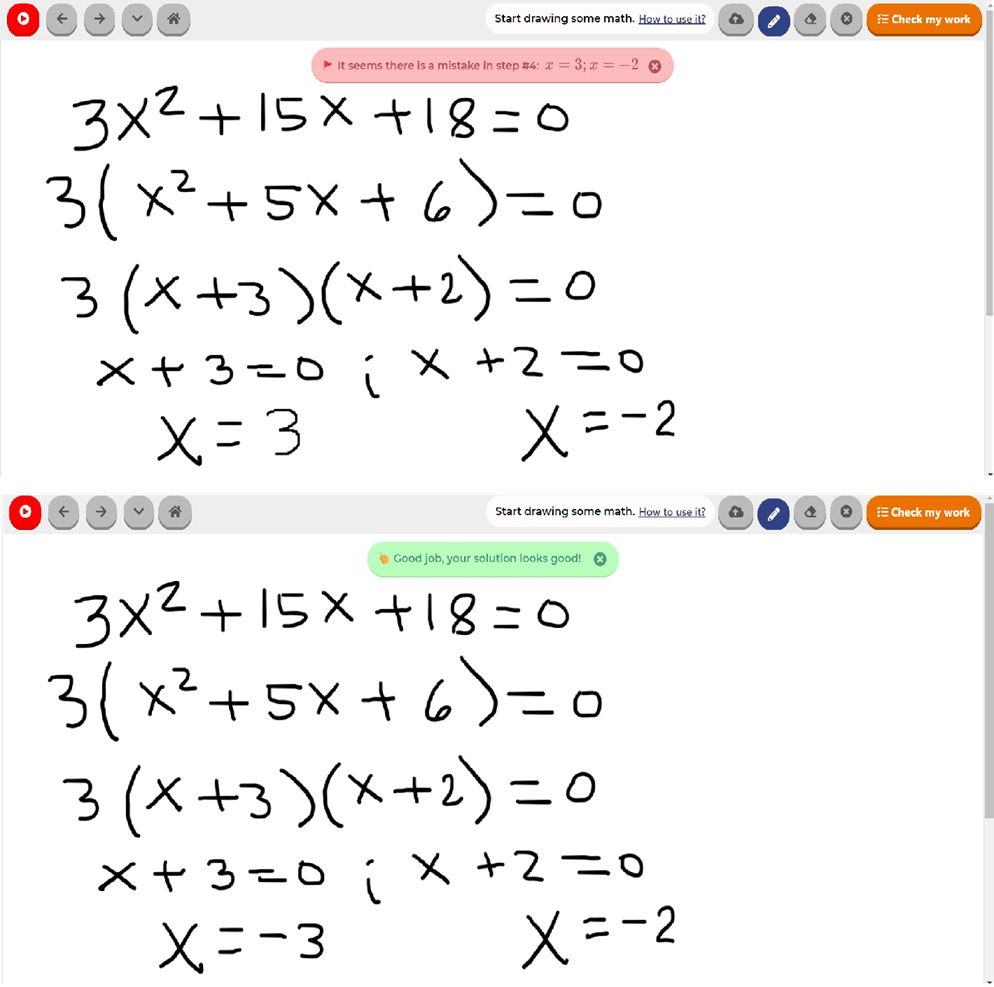
Endgültige Antwort auf das Problem
Schritt-für-Schritt-Lösung
Wie sollte ich dieses Problem lösen?
- Wählen Sie eine Option
- Produkt von Binomischen mit gemeinsamem Term
- FOIL Method
- Mehr laden...
Wenden Sie die Formel an: $\lim_{x\to c}\left(a^b\right)$$=\lim_{x\to c}\left(e^{b\ln\left(a\right)}\right)$, wobei $a=x$, $b=x$ und $c=0^{+}$
Learn how to solve grenzwerte problems step by step online.
$\lim_{x\to{0^{+}}}\left(e^{x\ln\left(x\right)}\right)$
Learn how to solve grenzwerte problems step by step online. (x)->(0^possign)lim(x^x). Wenden Sie die Formel an: \lim_{x\to c}\left(a^b\right)=\lim_{x\to c}\left(e^{b\ln\left(a\right)}\right), wobei a=x, b=x und c=0^{+}. Wenden Sie die Formel an: \lim_{x\to c}\left(a^b\right)={\left(\lim_{x\to c}\left(a\right)\right)}^{\lim_{x\to c}\left(b\right)}, wobei a=e, b=x\ln\left(x\right) und c=0^{+}. Wenden Sie die Formel an: \lim_{x\to c}\left(a\right)=a, wobei a=e und c=0^{+}. Schreiben Sie das Produkt innerhalb der Grenze als Bruch um.