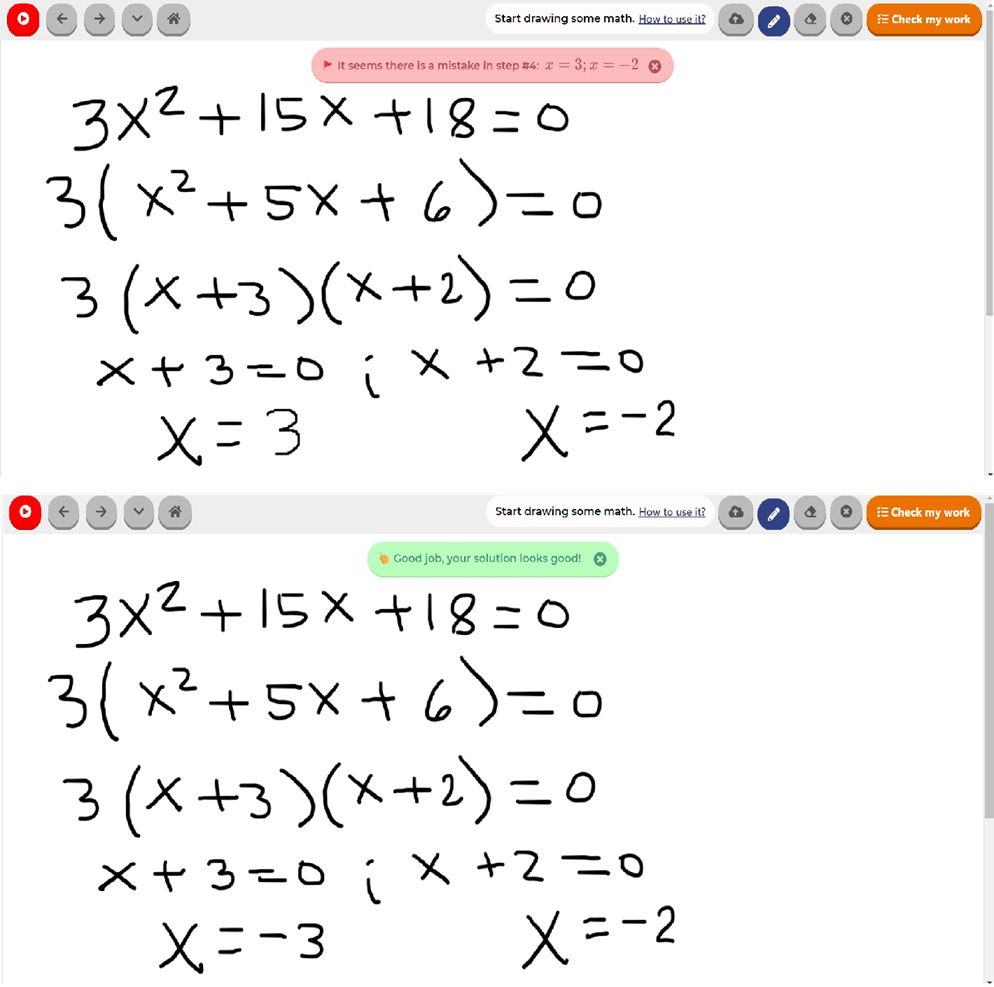
Endgültige Antwort auf das Problem
Schritt-für-Schritt-Lösung
Wie sollte ich dieses Problem lösen?
- Wählen Sie eine Option
- Produkt von Binomischen mit gemeinsamem Term
- FOIL Method
- Mehr laden...
Wenden Sie die Formel an: $\frac{a}{b}$$=\frac{\frac{a}{fgrow\left(b\right)}}{\frac{b}{fgrow\left(b\right)}}$, wobei $a=2x^3-3x^2+4$, $b=5x-x^2-7x^3$ und $a/b=\frac{2x^3-3x^2+4}{5x-x^2-7x^3}$
Learn how to solve lineare gleichungen mit zwei variablen problems step by step online.
$\lim_{x\to\infty }\left(\frac{\frac{2x^3-3x^2+4}{x^3}}{\frac{5x-x^2-7x^3}{x^3}}\right)$
Learn how to solve lineare gleichungen mit zwei variablen problems step by step online. (x)->(unendlich)lim((2x^3-3x^2+4)/(5x-x^2-7x^3)). Wenden Sie die Formel an: \frac{a}{b}=\frac{\frac{a}{fgrow\left(b\right)}}{\frac{b}{fgrow\left(b\right)}}, wobei a=2x^3-3x^2+4, b=5x-x^2-7x^3 und a/b=\frac{2x^3-3x^2+4}{5x-x^2-7x^3}. Wenden Sie die Formel an: \frac{a}{b}=\frac{splitfrac\left(a\right)}{splitfrac\left(b\right)}, wobei a=\frac{2x^3-3x^2+4}{x^3} und b=\frac{5x-x^2-7x^3}{x^3}. Wenden Sie die Formel an: \frac{a}{a}=1, wobei a/a=\frac{4}{x^3}. Wenden Sie die Formel an: \frac{a}{a^n}=\frac{1}{a^{\left(n-1\right)}}, wobei a=x und n=3.