Taschenrechner AI-Whiteboard Arbeitsblätter & Tests
Lösungen buchen
Algebra Baldor
Premium gehen Themen

Factor the expression $\frac{\sqrt{x^2}-16}{4}$

Schritt-für-Schritt-Lösung

Go!
Symbolischer Modus
Text-Modus
Go!
1
2
3
4
5
6
7
8
9
0
a
b
c
d
f
g
m
n
u
v
w
x
y
z
.
(◻)
+
-
×
◻/◻
/
÷
◻2
◻◻
√◻
√

◻√◻
◻√
∞
e
π
ln
log
log◻
lim
d/dx
D□x
∫
∫◻
|◻|
θ
=
>
<
>=
<=
sin
cos
tan
cot
sec
csc

asin
acos
atan
acot
asec
acsc

sinh
cosh
tanh
coth
sech
csch

asinh
acosh
atanh
acoth
asech
acsch

Lösung

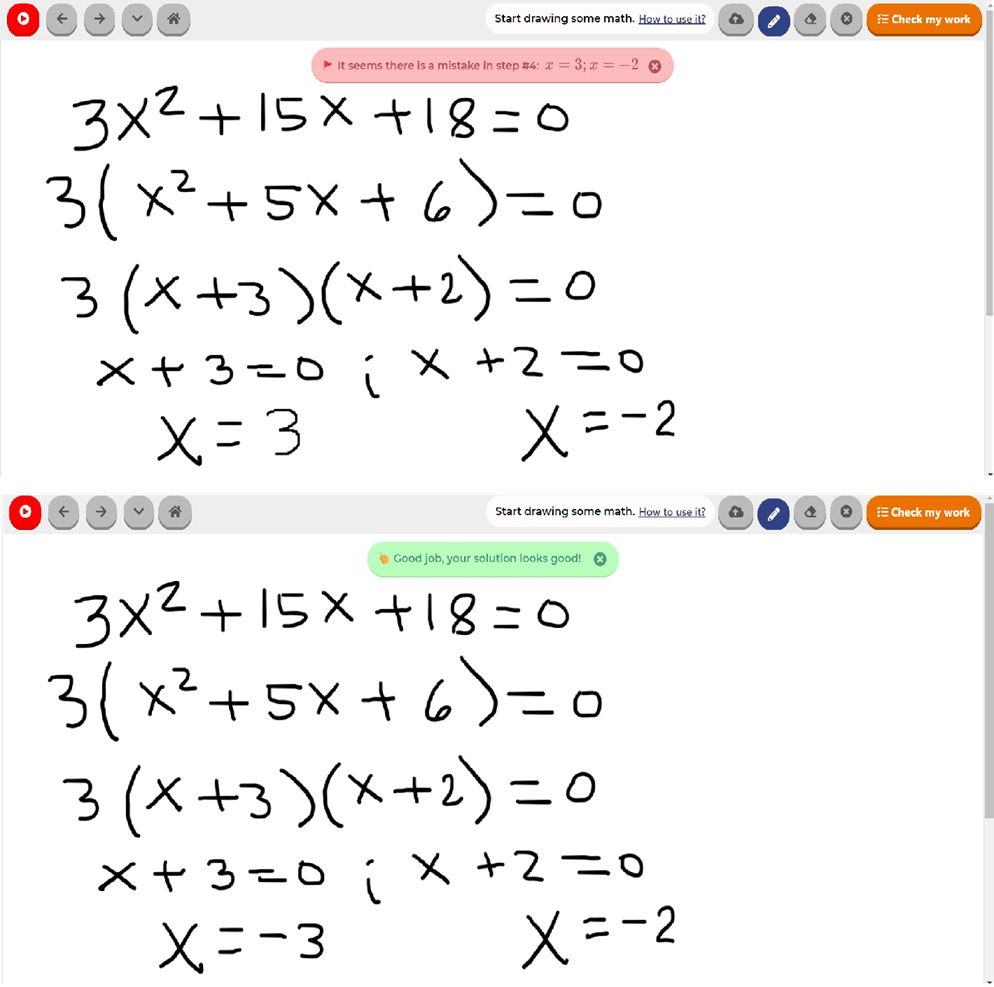
Wie sollte ich dieses Problem lösen?

  • Choose an option
  • Integrate by partial fractions
  • Product of Binomials with Common Term
  • FOIL Method
  • Integrate by substitution
  • Integrate by parts
  • Integrate using tabular integration
  • Integrate by trigonometric substitution
  • Weierstrass Substitution
  • Prove from LHS (left-hand side)
  • Mehr laden...
Sie können eine Methode nicht finden? Sagen Sie es uns, damit wir sie hinzufügen können.

Ableitung dieser Funktion

$\frac{d}{dx}\left(\frac{1-\tan\left(x\right)}{1+\tan\left(x\right)}\right)=\frac{\left(-1-\tan\left(x\right)\right)\sec\left(x\right)^2+\left(-1+\tan\left(x\right)\right)\sec\left(x\right)^2}{\left(1+\tan\left(x\right)\right)^2}$
Siehe Schritt-für-Schritt-Lösung

Sondieren Sie verschiedene Möglichkeiten, dieses Problem zu lösen

Das Lösen eines mathematischen Problems mit verschiedenen Methoden ist wichtig, weil es das Verständnis fördert, das kritische Denken anregt, mehrere Lösungen zulässt und Problemlösungsstrategien entwickelt. Mehr lesen

Helfen Sie uns mit Ihrem Feedback, uns zu verbessern!

Superlative für das Lernen von Mathe

Mit der Anmeldung erklären Sie sich mit SnapXams Bedingungen und Datenschutzbestimmungen.

Sie haben bereits ein Konto? Hier anmelden
Haben Sie Ihr Passwort vergessen?

Superlative für das Lernen von Mathe



Registrieren Sie sich hier, wenn Sie noch kein Konto haben.
Haben Sie Ihr Passwort vergessen?

Ihr persönlicher Mathe-Nachhilfelehrer. Angetrieben von KI

Verfügbar 24/7, 365.

Vollständige Schritt-für-Schritt-Lösungen für Mathe. Keine Werbung.

Enthält mehrere Lösungsmethoden.

Laden Sie Lösungen im PDF-Format herunter und behalten Sie sie für immer.

Unbegrenztes Üben mit unserem AI Whiteboard.

Premium-Zugang über unsere iOS- und Android-Apps.

Schließen Sie sich 500k+ Schülern bei der Lösung von Problemen an.

Wählen Sie Ihren Plan. Jederzeit kündigen.
Zahlen Sie $39,97 USD sicher mit Ihrer Zahlungsmethode.
Bitte warten Sie, während Ihre Zahlung bearbeitet wird.
Ein Konto erstellen