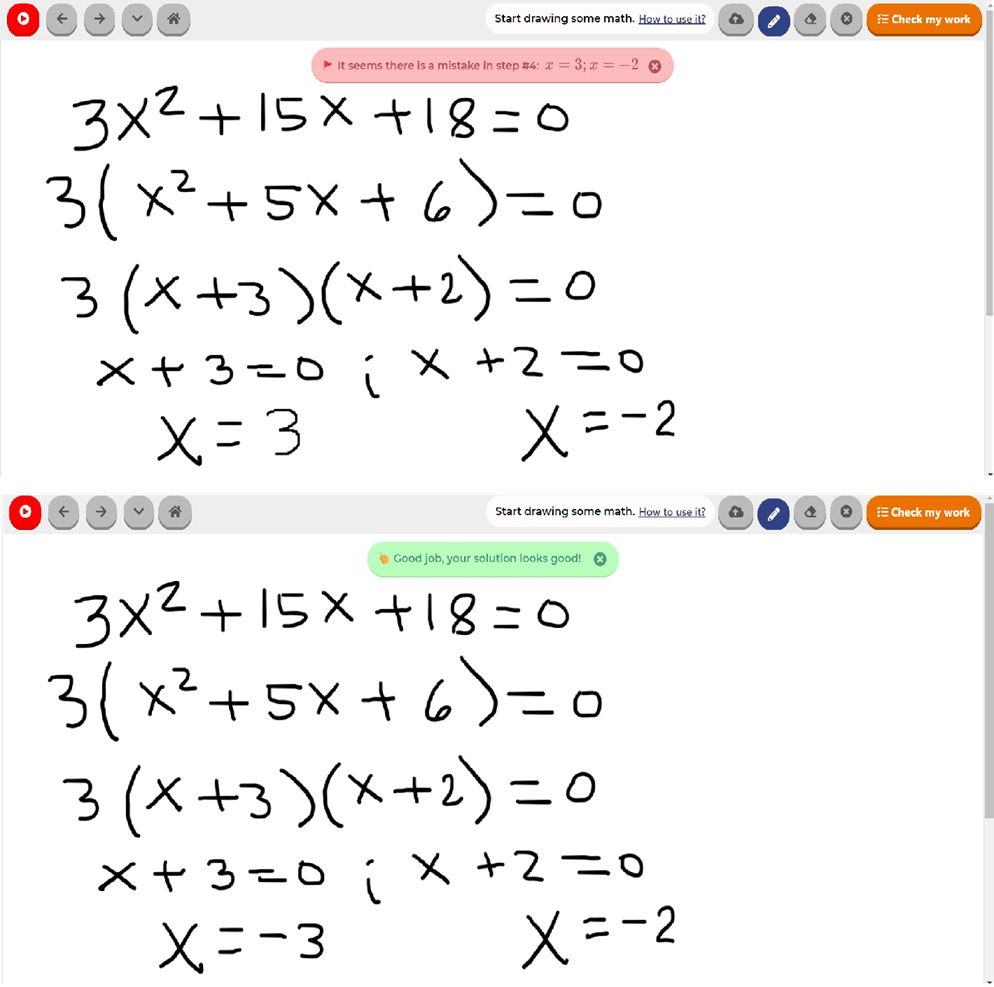
Endgültige Antwort auf das Problem
Schritt-für-Schritt-Lösung
Wie sollte ich dieses Problem lösen?
- Wählen Sie eine Option
- Weierstrass Substitution
- Produkt von Binomischen mit gemeinsamem Term
- Mehr laden...
Wenden Sie die Formel an: $e^x$$=\sum_{n=0}^{\infty } \frac{x^n}{n!}$, wobei $2.718281828459045=e$, $x=-x^2$ und $2.718281828459045^x=e^{-x^2}$
Learn how to solve definitive integrale problems step by step online.
$\int\sum_{0}^{2}_{n=0}^{\infty } \frac{\left(-x^2\right)^n}{n!}dx$
Learn how to solve definitive integrale problems step by step online. int(e^(-x^2))dx&0&2. Wenden Sie die Formel an: e^x=\sum_{n=0}^{\infty } \frac{x^n}{n!}, wobei 2.718281828459045=e, x=-x^2 und 2.718281828459045^x=e^{-x^2}. Wenden Sie die Formel an: \left(ab\right)^n=a^nb^n, wobei a=-1 und b=x^2. Simplify \left(x^2\right)^n using the power of a power property: \left(a^m\right)^n=a^{m\cdot n}. In the expression, m equals 2 and n equals n. Wenden Sie die Formel an: \int\sum_{a}^{b} \frac{x}{c}dx=\sum_{a}^{b} \frac{1}{c}\int xdx, wobei a=n=0, b=\infty , c=n! und x={\left(-1\right)}^nx^{2n}.