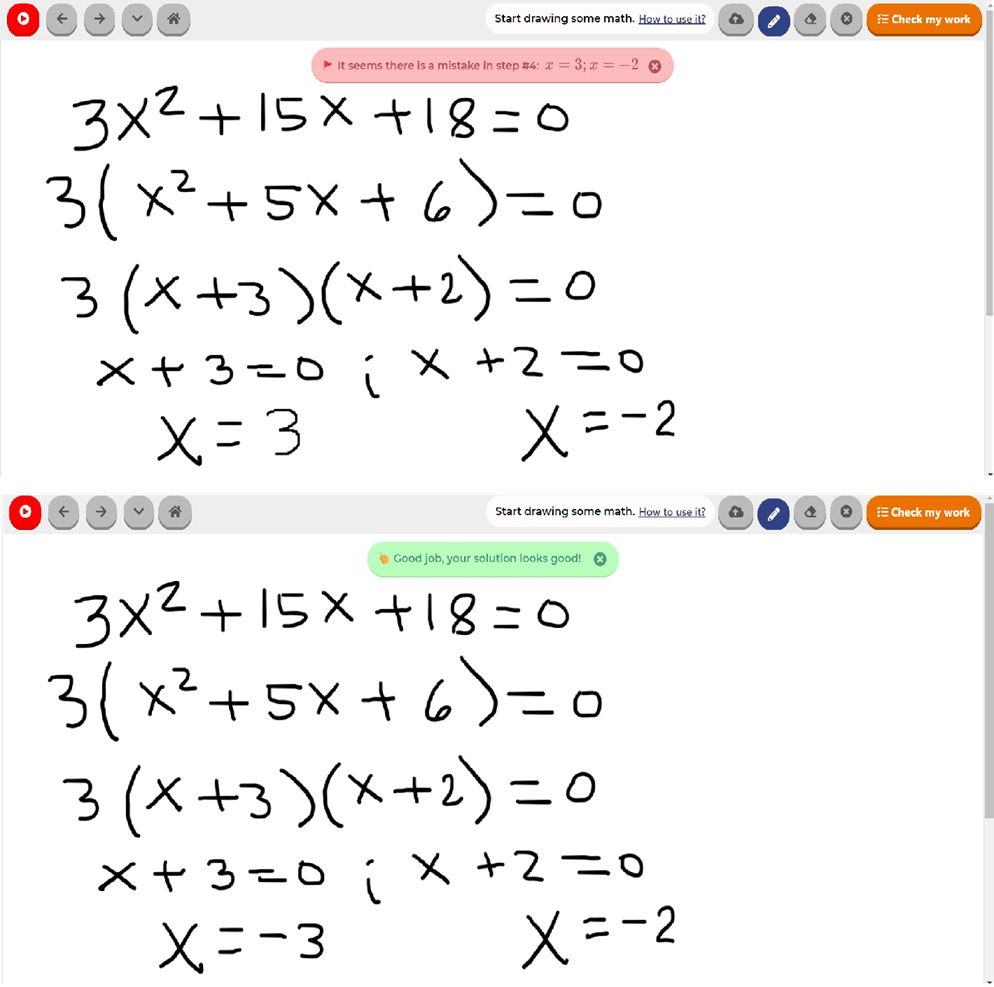
Endgültige Antwort auf das Problem
Schritt-für-Schritt-Lösung
Wie sollte ich dieses Problem lösen?
- Wählen Sie eine Option
- Produkt von Binomischen mit gemeinsamem Term
- FOIL Method
- Mehr laden...
Anwendung der trigonometrischen Identität: $\tan\left(\theta \right)$$=\frac{\sin\left(\theta \right)}{\cos\left(\theta \right)}$
Learn how to solve problems step by step online.
$\frac{1+\frac{\sin\left(x\right)}{\cos\left(x\right)}}{1+\cot\left(x\right)}$
Learn how to solve problems step by step online. (1+tan(x))/(1+cot(x)). Anwendung der trigonometrischen Identität: \tan\left(\theta \right)=\frac{\sin\left(\theta \right)}{\cos\left(\theta \right)}. Kombiniere alle Terme zu einem einzigen Bruch mit \cos\left(x\right) als gemeinsamen Nenner. Applying the trigonometric identity: \cot\left(\theta \right) = \frac{\cos\left(\theta \right)}{\sin\left(\theta \right)}. Wenden Sie die Formel an: a+\frac{b}{c}=\frac{b+ac}{c}, wobei a=1, b=\cos\left(x\right), c=\sin\left(x\right), a+b/c=1+\frac{\cos\left(x\right)}{\sin\left(x\right)} und b/c=\frac{\cos\left(x\right)}{\sin\left(x\right)}.